In this real life math example we will apply a double definite integral to approximate the lift on a simplified F1 wing. One of many Applied Math Examples.
Approximating Lift on F1 Wing With Double Definite Integral
This example will be used multiple times in my Applied Math Series. This article will focus on Double Integrals. If you were to ask a professor what a double integral was for, they would say to find the area between curves. Big help, right?
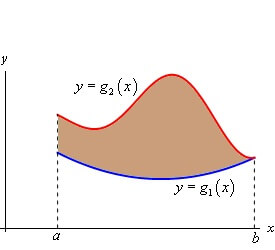
Didn’t think so.
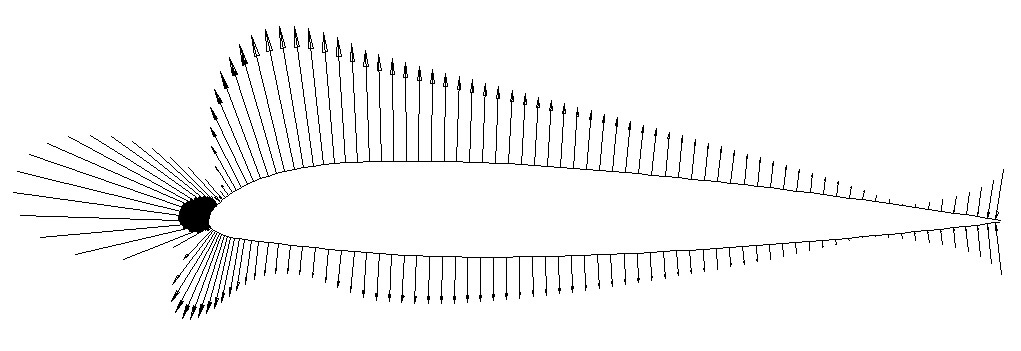
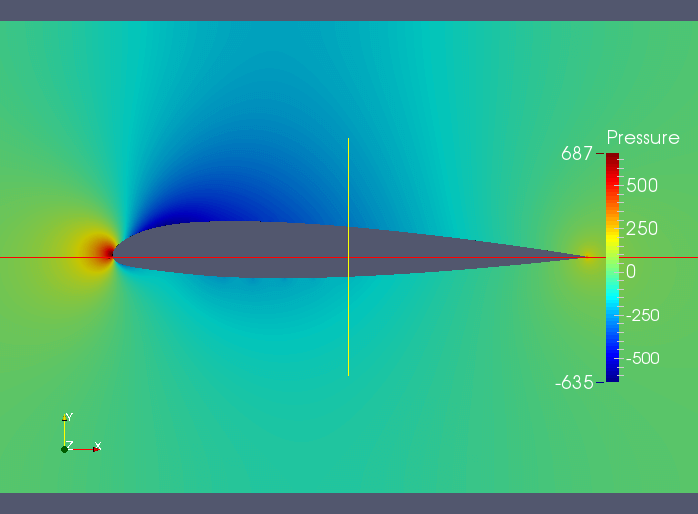
How can we put this “finding the area between curves” to use? There are many Double Integral Applications. In this example we want to find the Lift created by the NACA 23012 Wing by using a Double Integral. The model is shown below. Essentially the top (red) curve is the pressure on the bottom side of the wing, and the bottom (blue) curve is representing the pressure on the top side of the wing. This is the overall model. For just the area between the curves, see the Excel Scatterplot further below.
Data for Approximation
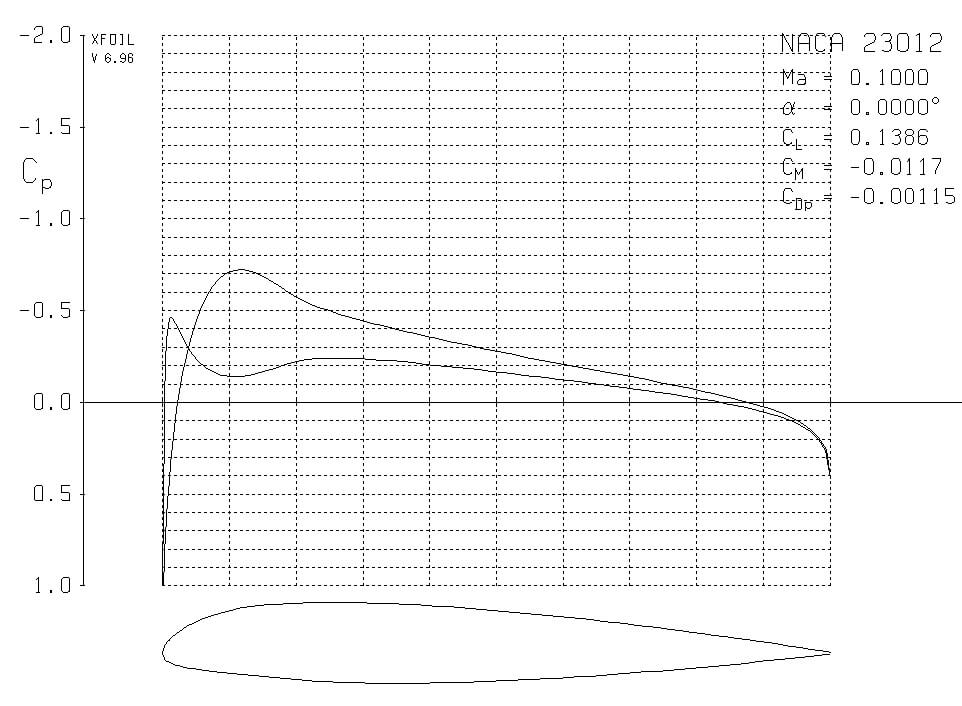
You can get the data points (X Y points from which to make a NACA 23012 Spline) from a website in my article on Great Aerodynamics Resources. I used XFOIL which is a free CFD software created by Mark Drela, and I just used the NACA23012 within the program (you can use an airfoil you model, or a standard NACA within the program). I ran the simulation and put the Coefficient of Pressure as a function of x into a text file. Next, I imported those data into Excel. I tinkered around with how to approximate the data in a way that it could be easily Integrated and I chose Polynomials. With the Polynomial Equations now approximating the Discrete Data brought in from the CFD Simulation using XFOIL on the NACA 23012, I was ready to take my Double Integrals to find the total Lift on the Wing.
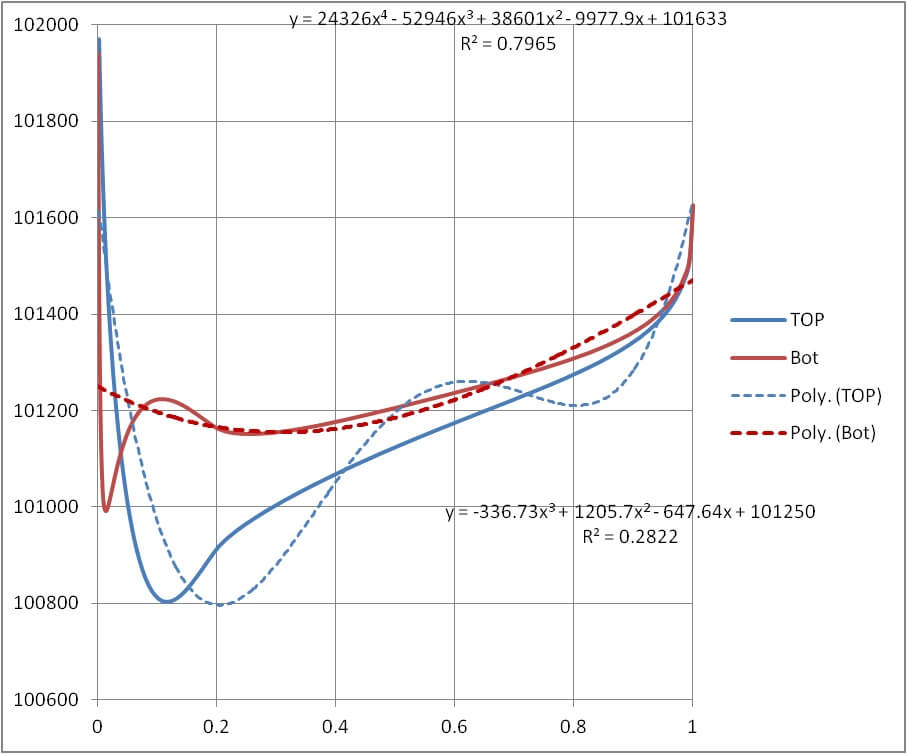
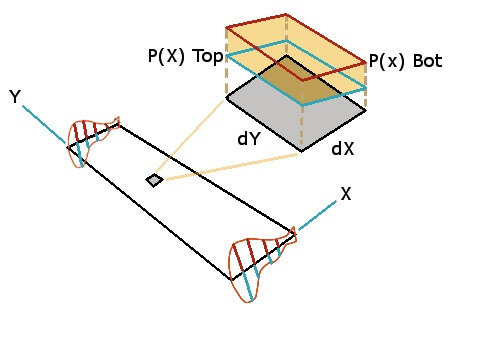
Here is the area we are actually trying to find. However analytically finding that area would be extremely difficult since the curve needed to approximate that function very well would certainly be a mess. Instead, I approximated the curve with the polynomials shown below. The curves are shown with dotted lines. That is the actual planar region we’ll be finding, in order to find an approximate value for the highlighted region below.
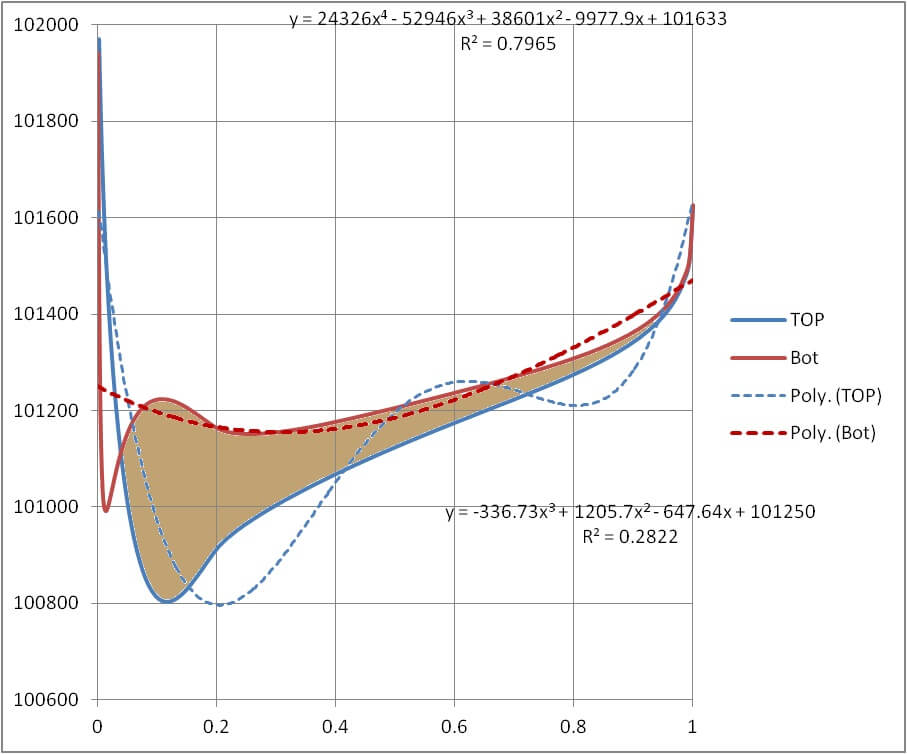
So to go along with the typical description you’ll get from a professor or a book, in a way you are looking for the area between two curves. However in this case, each of these curves represents the Static Pressure on the Wing as a function of position along the Chord.
Assumptions – Approximations for F1 Wing
Here are some of the assumptions used in this simulation:
- Inviscid Flow
- Incompressible Flow
- Integrated over flat surface
- Constant Pressure Profile over Full Span
- Ground Effect Not Considered
Model Parameters
- Mach Number = .1
- Chord = 1m
- Length = 1m
- 0 AOA
- Standard Atmosphere
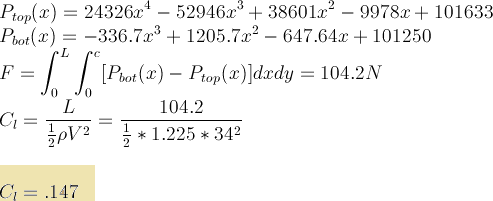
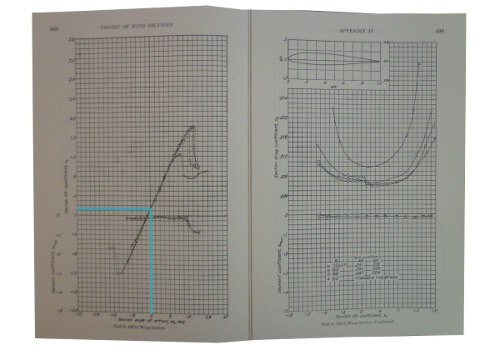
So with this approximation method, using Double Integrals on Polynomials we created to approximate the Static Pressure data we obtained from a CFD Simulation using XFOIL on the NACA 23012 Airfoil, we got a value of .147 for the Coefficient of lift. By my eye, the value obtained in Abbot[1] was .125, which gives an error of only 15% (for the airfoil, not for the finite length wing). Not too shabby for such a simple method! In later articles in this mini-series, which is itself within the Applied Math series, I’ll show better approximation methods to try to find a more accurate estimate of the lift the NACA 23012. I suspect Discrete Methods will produce better results, since the data is being recieved in a Discrete form. Many methods are available, and I hope to use this example to help fill in my Applied Math Examples List – Methods – Real World Uses list.
Double Integrals have many real world applications. I’ve shown you one today, and I intend to post many more of the real uses for Double Integrals in the articles to come.
References
[1] Abbot – Theory of Wing Sections – Check price on Amazon – https://amzn.to/2vNEi8B

